Estimating Decimal Products
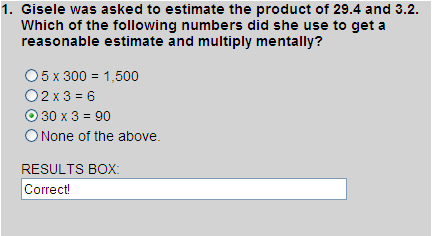
Using compatible numbers, 29.4 is changed to 30 and 3.2 is changed to 3. The product of 30 and 3 can be computed mentally.
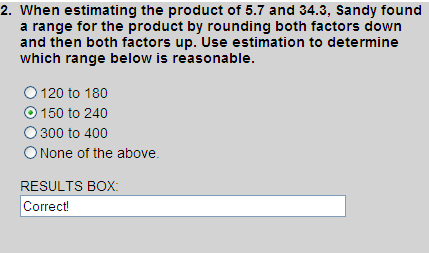
Rounding both factors down, we get:
05.7 
05
34.3 30
The product of 5 and 30 is 150.
Rounding both factors up, we get:
05.7 06
34.3 40
The product of 6 and 40 is 240.
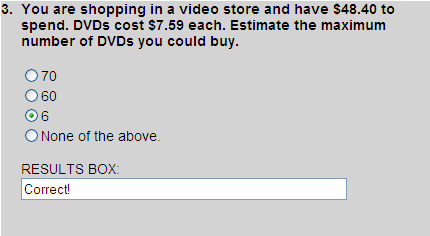
Using compatible numbers, $48.40 is changed to $48 and $7.59 is changed to $8. Working backwards, the product of $8 and 6 is $48.
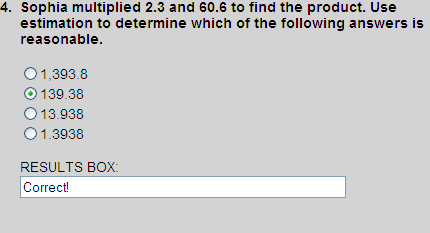
Using compatible numbers, 2.3 is changed to 2 and 60.6 is changed to 60. Thus, the estimated product is 120. Choice 2 makes sense since 139.38 is closest to our estimate of 120.
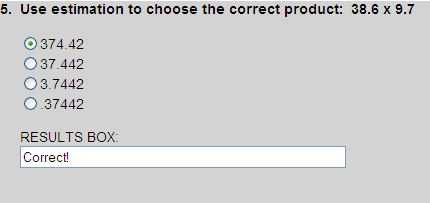
Using compatible numbers, 38.6 is changed to 40 and 9.7 is changed to 10. Thus, the estimated product is 400. Choice 1 makes sense since 374.42 is closest to our estimate of 400.
Multiplying Decimals and Whole Numbers
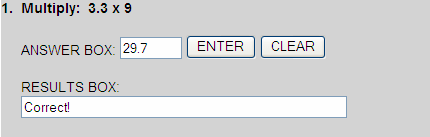
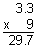
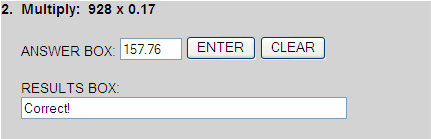
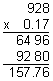
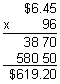
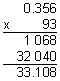
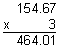
Multiplying Decimals
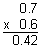
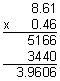
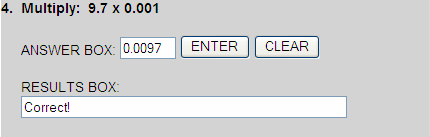
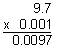
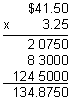
$134.8750 $134.88
Estimating Decimal Quotients
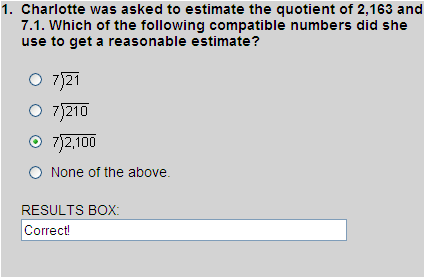
The number 2,163 is close to 2,100 and the number 7.1 is close to 7. Thus, using compatible numbers 2,100 and 7, we can find an estimated quotient.
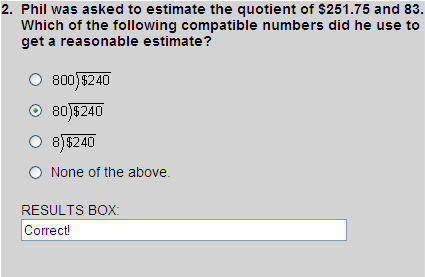
The number $251.75 is close to 240 and the number 83 is close to 80. Thus, using compatible numbers 240 and 80, we can find an estimated quotient.
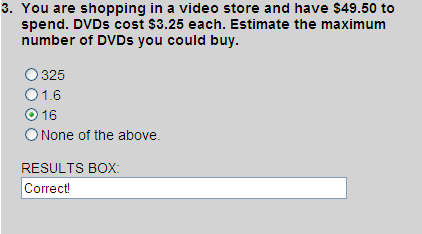
The number $49.50 is close to $48 and the number $3.25 is close to $3. Dividing $48 by $3, we get an estimated quotient of 16. Thus, choice 3 is the correct answer.
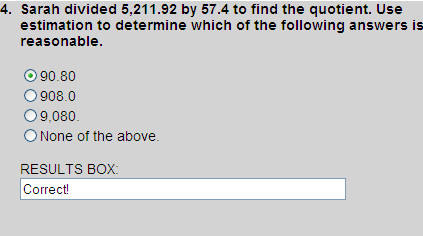
The number 5,211.92 is close to 5,400 and the number 57.4 is close to 60. Dividing 5,400 by 60, we get an estimated quotient of 90. Thus, choice 3 must be the correct answer, since it is closest to our estimated quotient of 90.
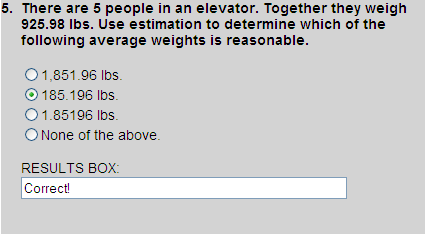
The number 925.98 is close to 900. Dividing 900 by 5, we get an estimated quotient of 180. Thus, choice 2 must be the correct answer, since it is closest to our estimated quotient of 180.
OR
The number 925.98 is close to 950. Dividing 950 by 5, we get an estimated quotient of 190. Thus, choice 2 must be the correct answer, since it is closest to our estimated quotient of 190.
Dividing Decimals By Whole Numbers
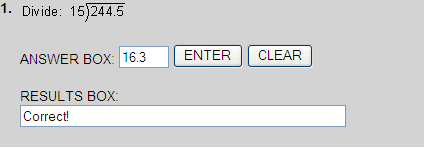
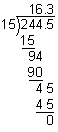
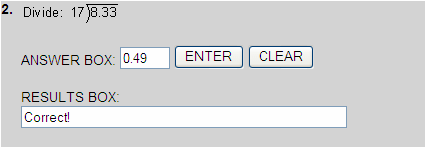
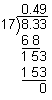
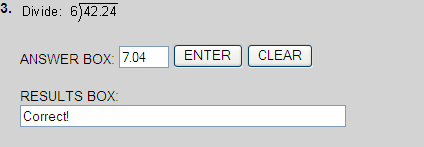
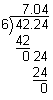
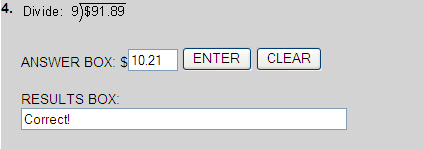
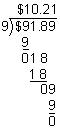
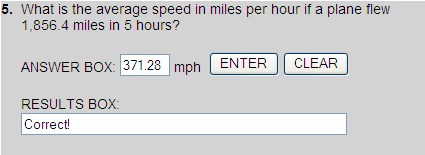
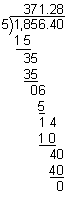
Rounding Decimal Quotients
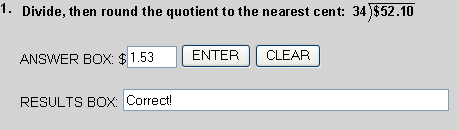
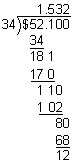
$1.532 $1.53
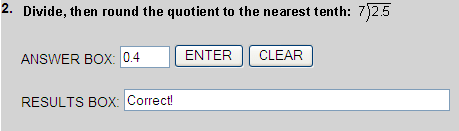
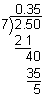
0.35 0.4
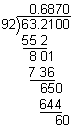
0.6870 0.687
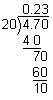
0.23 0.2
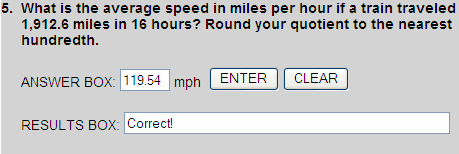
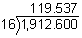
119.537 119.54
Dividing Decimals by Decimals
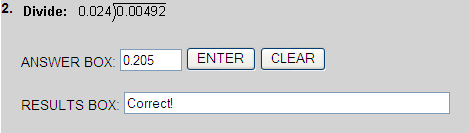
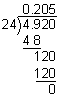
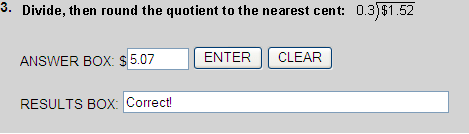
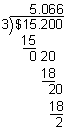
$5.066 $5.07
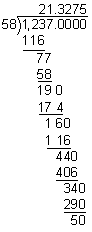
21.3275 21.328
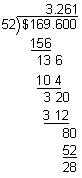
$3.261 $3.26
Solving More Decimal Word Problems
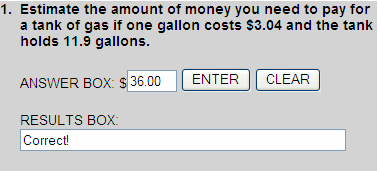
$3.04 $3
11.9 12
$3 x 12 = $36
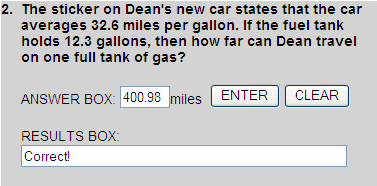
32.6 x 12.3 = 400.98
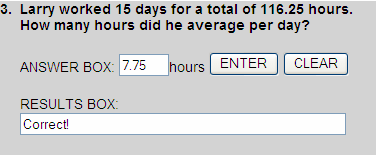
116.25 ÷ 15 = 7.75
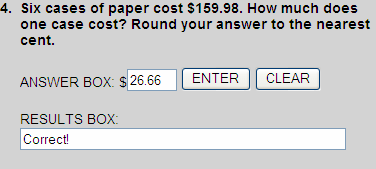
$159.98 ÷ 6 = $26.663
$26.663 $26.66
51.78 ÷ 2.54 = 20.3858
20.3858 20.386
Practice Exercises
8 x 7 = 56, so choice 2 is correct.
40 x 0.4 = 16, so choice 3 is correct.
The number 1,000 is a power of 10. Multiplying by 1,000 is the same as moving the decimal point 3 places to the right. So choice 4 is correct.
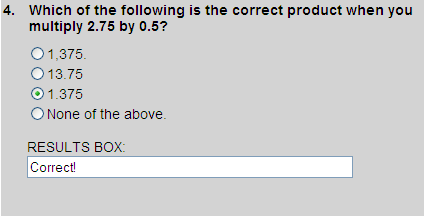
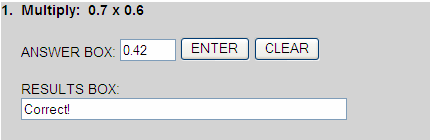
2.75 x 0.5 equals 1.375. So choice 3 is correct.
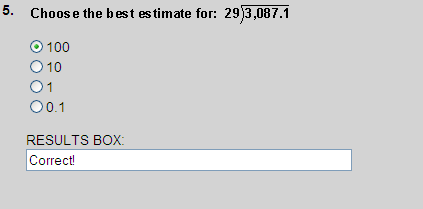
3,000 ÷ 30 = 100. So choice 1 is correct.
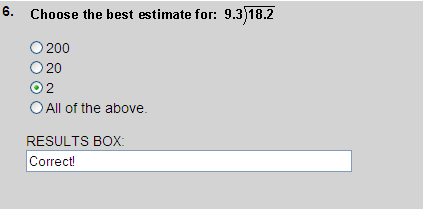
18 ÷ 9 = 2, so choice 3 is correct.
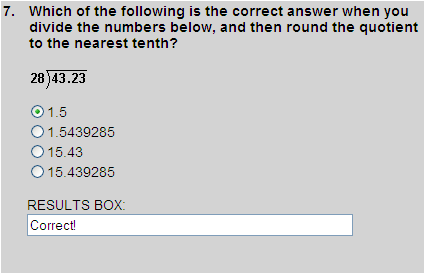
43.23 ÷ 28 = 1.54
1.54 1.5
So choice 1 is correct.
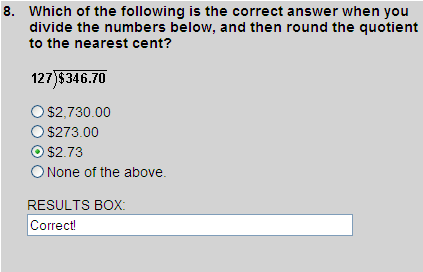
$346.70 ÷ 127 = $2.729
$2.729 $2.73
So choice 3 is correct.
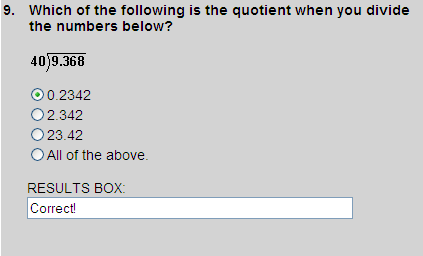
9.368 ÷ 40 = 0.2342, so choice 1 is correct.
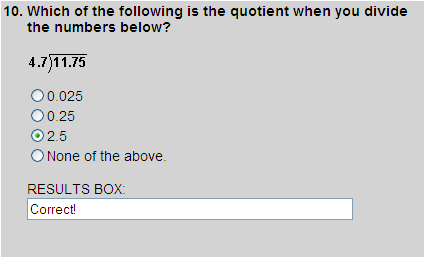
11.75 ÷ 4.7 is the same as 117.5 ÷ 47, the quotient of which is 2.5. So choice 3 is correct.
Challenge Exercises
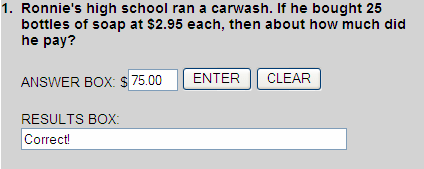
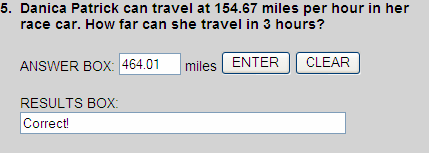
Multiply 25 by $3 to get an estimated product of $75.
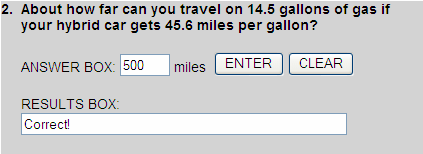
We can round one factor up and one factor down to find an estimated product. There are two ways of doing this:
14.5 10
45.6 50
10 x 50 = 500
OR
14.5 20
45.6 40
20 x 40 = 800
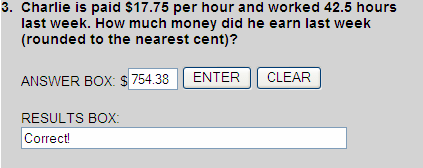
$17.75 x 42.5 = $754.375
$754.375 $754.38
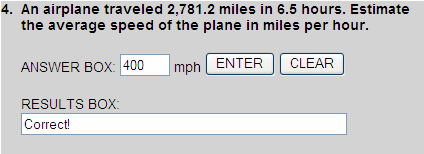
We can round use compatible numbers find an estimated quotient. There are two ways of doing this:
2,781.2 2,800
6.5 7
2,800 ÷ 7 = 400
OR
2,781.2 3,000
6.5 6
3,000 ÷ 6 = 500
Note: 500 mph is also correct.
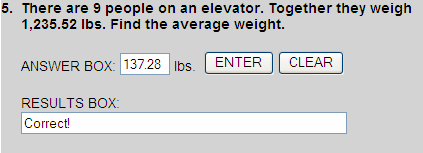
1,235.52 lbs. ÷ 9 = 137.28 lbs.
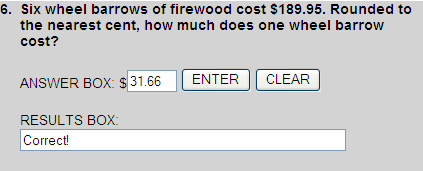
$189.95 ÷ 6 = $31.658
$31.658 $31.66
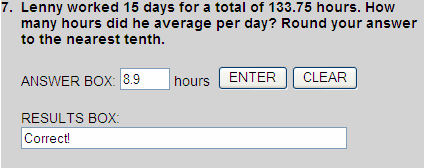
133.75 ÷ 15 = 8.91
8.91 8.9
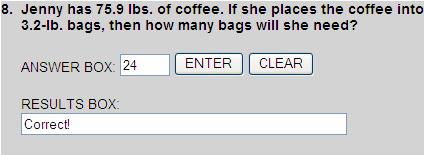
75.9 ÷ 3.2 = 23.71875
When dealing with bags, we can only count whole numbers. Therefore, Jenny will need 24 bags.
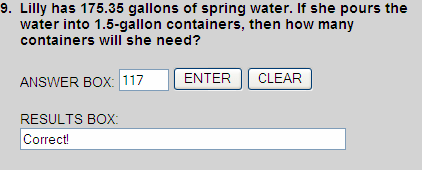
175.35 ÷ 1.5 = 116.9
When dealing with containers, we can only count whole numbers. Therefore, Lilly will need 117 bags.
$4,189.36 ÷ $804.10 = 5.20
5.20 5.2
